Buffer Optimization - Mathematical Models
As random phenomena such as breakdowns or the variability of the processing times result in a loss of throughput, the stations in an asynchronous flow production system are usually decoupled with the help of buffers. A buffer space protects the system against machine breakdowns or unevenness or randomness in production speed at the inter-dependent stations.
As a single buffer unit may represent a considerable amount of investment, up to several thousand US-Dollars, and also requires scarce factory space, and as the planners normally must treat the throughput of the production system to be planned as a datum, they usually aim at minimizing the total number of buffer spaces, $B$, w.r.t. a desired throughput level $X_{\min}$. Let $N\; (n=1,2,\ldots,N)$ be the number of buffers and $B_n$ be the size of buffer $n$, then the buffer optimization problem is to find the minimum total number of buffer spaces required to achieve a target throughput of the system:
Minimize $B = \displaystyle{\sum_{n=1}^{N}} B_n$
subject to
$X(B_1,B_2,\ldots,B_N)\geq X_{\min}$
In the literature, this problem is called primal problem. Usually, there is a slightly different formulation based on the fact that each buffer is associated with a station (i.e. buffer $n$ is the buffer located in front of station $m$). Then, if $M\; (m=1,2,\ldots,M)$ is the number of stations and the buffer in front of station 1 is excluded from the optimization, we have
Minimize $B = \displaystyle{\sum_{m=2}^{M}} B_m$
subject to
$X(B_2,B_3,\ldots,B_M)\geq X_{\min}$
The above primal problem is interrelated with the so-called dual problem which reads as follows
Maximize $X(B_1,B_2,\ldots,B_N)$
subject to
$\displaystyle{\sum_{n=1}^{N}} B_n = B$
The dual problem is to allocate a given total number of buffers such that the throughput of the system is maximized.
The following figure shows the development of the throughput of a flow production system as a function of total buffer size.
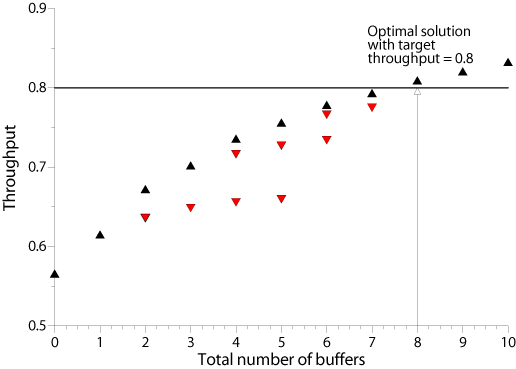
The black triangles show the development of the throughput as a function of the total number $B$ of buffer spaces in the system. If the target throughput is, say, 0.8, then we can draw a horizontal line and find the minum number of buffers required, which is the solution to the primal problem. However, this requires that we know the curve marked by the black triangles. The black triangles mark the efficient frontier of the system. Each black triangle is associated with a given total number of buffers. However, a given total number of buffers can be allocated optimally (with maximum throughput), not so optimally, or even very badly among the stations. The red triangles show the throughput of a given total number of buffers, if these are allocated among the stations in a suboptimal fashion. Finding the throughput-maximal allocation of a given total number of buffers is the dual problem. Thus, in order to solve the primal problem, we must be able to compute the positions of the black triangles which in turn requires the optimum solution of the dual problem for a given total number of buffers.
Thus, buffer optimization deals with the following questions:
| 1. | How many buffers are required in the flow production systems in order to achieve a target production rate? | This is called the Primal Problem. |
| 2 | How should these buffers be allocated among the stations? | This is called the Dual Problem. |
As noted above, both questions are tightly related. Obviously, solving the dual and/or the primal problem requires the performance evaluation of a significant number of candidate system configurations, including the buffer allocations. Hence, being able to quickly evaluate a given candidate system configuration is a prerequisite for finding the optimum configuration of a flow production system.
In the literature, many solution approaches have been presented. POM Flowline Optimizer uses a proprietary solution procedure which solves very large buffer optimization problems in a few seconds.
